题目内容
20.暑假期间,某甜品店为了回馈顾客和促销,准备推出掷骰子(投掷各方面数字为1到6的均匀正方体看面朝上的点数)赢积分劵的活动,游戏规则如下:顾客每次消费后,可同时投掷两枚骰子一次,两枚骰子点数之和写作a,两枚骰子点数之差的绝对值记作x,若0≤x≤2,则n=x;若3≤x≤5,则n=x-3;顾客获得的奖券金额为an元,用于在以后来店消费中抵用现金.(1)用树状图或列表法写出a的所有结果;
(2)计算顾客获得1元奖券的概率;
(3)计算顾客获得100元以上(含100元)奖券的概率.
分析 (1)列表可得;
(2)顾客获得1元奖券时n=0或1或2,而a≠0,可得n=0,即可得概率;
(3)若要获得100元以上(含100元)奖券则n=2,a=10或11或12,而总结果数为36×3=108,根据概率公式可得.
解答 解:(1)列表得:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(2)由题意可得:n=0或1或2,
∵a≠0,
∴只有当n=0时,an=1,
∴顾客获得1元奖券的概率为:$\frac{1}{3}$;
(3)根据题意,可知n=2,a=10或11或12,
∵a的结果数有36个,n的结果数有3个,
∴an的所有结果数为36×3=108个,
∵获得100元以上(含100元)奖券的结果数为6个,
∴获得100元以上(含100元)奖券的概率为$\frac{6}{108}$=$\frac{1}{18}$.
点评 本题考查借助树状图或列表法求概率.解题的关键是理解题意得出所获奖券所对应的结果数与总结果数.

练习册系列答案
相关题目
8.下列方程中,你最喜欢的一个一元二次方程是( )
| A. | $\frac{1}{4}{x^2}$-x=9 | B. | x3-x2+40=0 | C. | $\frac{4}{x-1}$=3 | D. | 3x3-2xy+y2=0 |
10.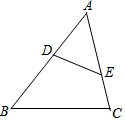 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{BC}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答:
将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9.寻找规律,然后解答: