题目内容
18. 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
分析 延长AF到H,使AF=FH,连结BH.首先依据SS证明△AFC≌△HFB,接下来证明∠ABH=∠DAE,然后依据SAS证明△ABH≌△DAE,依据全等三角形的性质可得到AF与DE的数量关系和位置关系.
解答 解:DE=2AF且DE⊥AF.
理由:延长AF到H,使AF=FH,连结BH.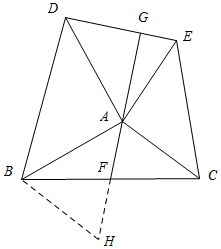
在△AFC和△HFB中,$\left\{\begin{array}{l}{AF=FH}\\{∠AFC=∠HFB}\\{BF=FC}\end{array}\right.$,
∴△AFC≌△HFB.
∴AC=BH,∠ACF=∠FBH.
∴∠ABH=180°-∠BAC.
∵△ABD和△ACE均为等腰直角三角形,
∴AD=AB,AE=AC,∠BAD=∠EAC=90°.
∴AE=BH,∠DAE=180°-∠BC.
∴∠ABH=∠DAE.
在△ABH和△DAE中$\left\{\begin{array}{l}{AB=AD}\\{∠ABH=∠DAE}\\{BH=AE}\end{array}\right.$,
∴△ABH≌△DAE.
∴AH=ED,∠BAH=∠ADE.
∵AH=2AF,∠BAH+∠DAG=90°,
∴DE=2AF,∠GAD+∠GDA=90°,
∴AF⊥DE.
点评 本题主要考查的是全等三角形的性质和判定、等腰直角三角形的性质,掌握本题的辅助线的做法是解题的关键.

练习册系列答案
相关题目
 已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.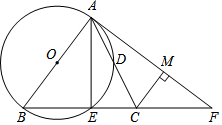 如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.
如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE. 如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度.
如图,△ABC中,BC=4,∠BAC=60°,且AB≠AC,若∠A的内外角平分线分别交BC的中垂线于D、E,试求DE的长度.