题目内容
10.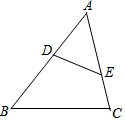 已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
已知,如图,在△ABC中,∠ADE=∠C,则下列等式成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{BC}$ | B. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AB}$ |
分析 先根据相似三角形的判定定理求出△ADE∽△ACB,再根据其对应边成比例解答即可.
解答 解:∵在△ABC中,∠ADE=∠C,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$.
故选C.
点评 本题主要考查了相似三角形的判定与性质,熟知有两个角对应相等的三角形相似,相似三角形的对应边的比相等是解答此题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
18.下列四个图形中属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如表:
则该函数图象的对称轴是直线x=-2.
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
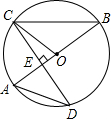 如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.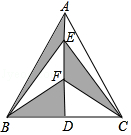 如图,在等边三角形ABC中,AD是BC边上的高,点E、F是AD上的 两点,AB=8cm,AD=4$\sqrt{3}$cm,则图中阴影部分的面积是8$\sqrt{3}$cm.
如图,在等边三角形ABC中,AD是BC边上的高,点E、F是AD上的 两点,AB=8cm,AD=4$\sqrt{3}$cm,则图中阴影部分的面积是8$\sqrt{3}$cm.