题目内容
3.已知一个直角三角形的一条直角边长为$\frac{3}{2}$,斜边长为$\frac{5}{2}$,它的面积是$\frac{3}{2}$.分析 先根据一个直角三角形的一条直角边长和斜边长,利用勾股定理计算出另一直角边长,然后即可求出此三角形面积.
解答 解;∵一个直角三角形的一条直角边长为$\frac{3}{2}$,斜边长为$\frac{5}{2}$,
∴由勾股定理得另一直角边长=$\sqrt{(\frac{5}{2})^{2}-(\frac{3}{2})^{2}}$=2,
∴直角三角形的面积=$\frac{1}{2}$×$\frac{3}{2}$×2=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题主要考查学生对勾股定理和三角形面积的理解和掌握;利用勾股定理计算出另一直角边长是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.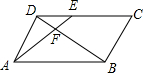 如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )
 如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )| A. | 4:25 | B. | 2:5 | C. | 2:7 | D. | 4:29 |
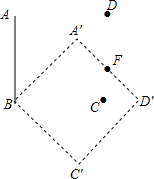 如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中:
如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中: