题目内容
18.化简求值:(1)已知:x=$\frac{2}{{\sqrt{3}-1}}$,求x2-x+1的值.
(2)已知:a=$\frac{{2-\sqrt{3}}}{{2+\sqrt{3}}}$,b=$\frac{{2+\sqrt{3}}}{{2-\sqrt{3}}}$,求:$\sqrt{{a^2}+4ab+{b^2}}$的值.
分析 (1)首先把x化简,得出x-1的值,再由完全平方公式即可得出结果;
(2)首先把a和b化简,得出a+b的值,再根据完全平方公式得出a2+4ab+b2的值,即可得出结果.
解答 解:(1)∵x=$\frac{2}{{\sqrt{3}-1}}$=$\sqrt{3}$+1,
∴x-1=$\sqrt{3}$,
∴x2-x+1=(x-1)2+x=3+$\sqrt{3}$+1=4+$\sqrt{3}$;
(2)∵a=$\frac{{2-\sqrt{3}}}{{2+\sqrt{3}}}$=(2-$\sqrt{3}$)2=7-4$\sqrt{3}$,
b=$\frac{{2+\sqrt{3}}}{{2-\sqrt{3}}}$=(2+$\sqrt{3}$)2=7+4$\sqrt{3}$,
∴a+b=14,ab=1,
∴a2+4ab+b2=(a+b)2+2ab=142+2×1=198,
∴$\sqrt{{a^2}+4ab+{b^2}}$=$\sqrt{198}$=3$\sqrt{22}$.
点评 本题考查了二次根式的化简求值、完全平方公式;熟练掌握二次根式的化简和完全平方公式是解决问题的关键.

练习册系列答案
相关题目
9.下列命题是正确的有( )
| A. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| B. | 三角形的内心到三角形各顶点的距离都相等 | |
| C. | 过同一平面内的任意三点有且仅有一个圆 | |
| D. | 半径相等的两个半圆是等弧 |
6.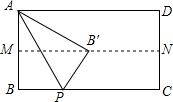 如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
 如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )
如图,点M、N分别是矩形ABCD的边AB和CD的中点,P是BC上的一点,△APB沿AP翻折后,点B恰好落在MN上,则∠APB=( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
 已知a,b,c在数轴上对应的点的位置如图所示:化简:|b+c|+|a+c|-|b-a|-|a+b+c|.
已知a,b,c在数轴上对应的点的位置如图所示:化简:|b+c|+|a+c|-|b-a|-|a+b+c|.