题目内容
13．
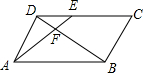如图，在平行四边形ABCD中，E为CD上一点，连结AE，BD，且AE，BD交于点F，S△DEF：S△ABF=4：25，求DE：DC的值为（ ）| A． | 4：25 | B． | 2：5 | C． | 2：7 | D． | 4：29 |
分析 由条件可证明△DEF∽△BAF，结合面积比可求得相似比，可求得答案．
解答 解：∵四边形ABCD为平行四边形，
∴DE∥AB，
∴△DEF∽△BAF，
∴S△DEF：S△ABF=（$\frac{DE}{AB}$）2=4：25，
∴$\frac{DE}{AB}$=$\frac{DE}{CD}$=$\frac{2}{5}$，
故选B．
点评 本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
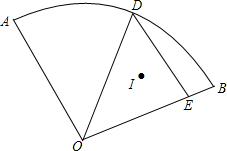如图所示扇形AOB中，∠AOB=90°，OA=OB=6，D为弧上一动点，过D作DE∥OA交OB于点E．I为△ODE的内心，当点D运动时，I也随着运动．则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$．
已知a，b，c在数轴上对应的点的位置如图所示：化简：|b+c|+|a+c|-|b-a|-|a+b+c|．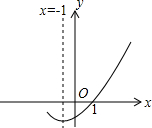
已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论正确的有（ ）个．①a+b+c=0；②ax2+bx+c=0的两根分别为-3和1；③b＞2a；④a-2b+c＞0．