题目内容

14．已知点A（a1，b1），点B（a2，b2）两点都在二次函数y=-x2+6的图象上，且a1＜$a_2^{\;}$＜0，那么b1＜b2．

分析 先根据函数解析式确定出对称轴为y轴，再根据二次函数的增减性，x＜0时，y随x的增大而增大解答．

解答 解：∵y=-x2+6，
∴二次函数图象的开口向下，对称轴为y轴，
∵a1＜$a_2^{\;}$＜0，
∴b1＜b2．
故答案为：＜．

点评 本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性，求出对称轴解析式是解题的关键．

练习册系列答案
相关题目
4．在代数式$\frac{2}{3}$x，$\frac{3x}{x+4}$，$\frac{{3{x^2}-5}}{2x}$，$\frac{2}{π}$，$\frac{1}{2}x-\frac{1}{3}$y，$\frac{2b}{{3{a^2}}}$中，分式共有（　　）个．
A．2B．3C．4D．5
5．如图，△ABC的顶点在格点上，且点A（-5，-1），点C（-1，-2）．以原点O为位似中心，位似比为2，在第一象限内将△ABC放大，画出△ABC放大后的图形△A′B′C′并写出△A′B′C′各顶点坐标．
2．定义：直线y=ax+b（a≠0）称作抛物线y=ax2+bx（a≠0）的关联直线．根据定义回答以下问题：
（1）已知抛物线y=ax2+bx（a≠0）的关联直线为y=x+2，则该抛物线的顶点坐标为（-1，-1）；
（2）求证：抛物线y=ax2+bx与其关联直线一定有公共点；
（3）当a=1时，请写出抛物线y=ax2+bx与其关联直线所共有的特征（写出一条即可）．
9．下列命题是正确的有（　　）
A．平分弦的直径垂直于弦，并且平分弦所对的两条弧
B．三角形的内心到三角形各顶点的距离都相等
C．过同一平面内的任意三点有且仅有一个圆
D．半径相等的两个半圆是等弧
19．已知函数y=x2+bx-1的图象经过点（3，2）．
（1）求这个函数的解析式；
（2）直接写出它的顶点坐标和对称轴．
6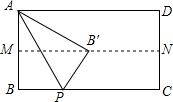．如图，点M、N分别是矩形ABCD的边AB和CD的中点，P是BC上的一点，△APB沿AP翻折后，点B恰好落在MN上，则∠APB=（　　）
A．30°B．45°C．60°D．无法确定
3．已知一个直角三角形的一条直角边长为$\frac{3}{2}$，斜边长为$\frac{5}{2}$，它的面积是$\frac{3}{2}$．
4．如图，C，D是线段AB上两点，若CB=4cm，DB=7cm，且D是AC的中点，则AD的长等于3cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网