题目内容
10.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )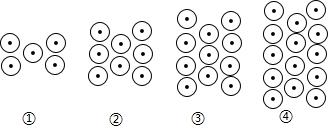
| A. | 2998 | B. | 3001 | C. | 3002 | D. | 3005 |
分析 将原图形中基本图形划分为中间部分和两边部分,中间基本图形个数等于序数,两边基本图形的个数和等于序数加1的两倍,据此规律可得答案.
解答 解:∵第①个图形中基本图形的个数5=1+2×2,
第②个图形中基本图形的个数8=2+2×3,
第③个图形中基本图形的个数11=3+2×4,
第④个图形中基本图形的个数14=4+2×5,
…
∴第n个图形中基本图形的个数为n+2(n+1)=3n+2
当n=1001时,3n+2=3×1001+2=3005,
故选:D.
点评 本题考查了图形的变化类,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,解决本题的关键在于将原图形划分得出基本图形的数字规律.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )
| A. | 当r=2时,直线AB与⊙C相交 | B. | 当r=3时,直线AB与⊙C相离 | ||
| C. | 当r=2.4时,直线AB与⊙C相切 | D. | 当r=4时,直线AB与⊙C相切 |
18.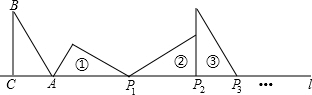 如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
 如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )| A. | 2016+671$\sqrt{3}$ | B. | 2016+672$\sqrt{3}$ | C. | 2017+672$\sqrt{3}$ | D. | 2016+673$\sqrt{3}$ |
5.已知代数式x+2y的值是4,则代数式2x+4y+1的值是( )
| A. | 4 | B. | 6 | C. | 9 | D. | 不能确定 |
2.城市轨道交通的建设为市民的出行提供了很多便利,根据成都市城市轨道交通第三期的建设规定(2016至2020年),至2020年,我市将形成13条线路,总长508000米的轨道交通网.将508000用科学记数法表示为( )
| A. | 5.08×106 | B. | 5.08×105 | C. | 0.508×106 | D. | 50.8×104 |
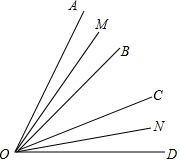 如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.
如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.