题目内容
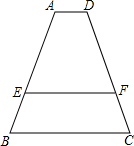 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=考点:黄金分割,平行线分线段成比例
专题:计算题
分析:过D点作DH∥AB交BC于H,交EF于Q,如图,易得四边形AEQD和四边形ABHD都是平行四边形,则BH=EQ=AD=2,AE=DQ,DH=AB,得到CH=BC-BH=4,由于AE2=AB•EB,则E点为AB的黄金分割点,所以AE:AB=
,即DQ:DH=
,再利用平行线分线段成比例定理得到QF:HC=DQ:DH=
,可计算出QF=2
-2,于是有EF=EQ+QF=2
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 5 |
| 5 |
解答: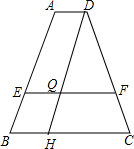 解:过D点作DH∥AB交BC于H,交EF于Q,如图,
解:过D点作DH∥AB交BC于H,交EF于Q,如图,
∵AD∥EF∥BH,
∴四边形AEQD和四边形ABHD都是平行四边形,
∴BH=EQ=AD=2,AE=DQ,DH=AB,
∴CH=BC-BH=6-2=4,
∵AE2=AB•EB,
∴AE:AB=
,
∴DQ:DH=
,
∵QF∥CH,
∴QF:HC=DQ:DH=
,
∴QF=
HC=2
-2,
∴EF=EQ+QF=2
.
故答案为2
.
 解:过D点作DH∥AB交BC于H,交EF于Q,如图,
解:过D点作DH∥AB交BC于H,交EF于Q,如图,∵AD∥EF∥BH,
∴四边形AEQD和四边形ABHD都是平行四边形,
∴BH=EQ=AD=2,AE=DQ,DH=AB,
∴CH=BC-BH=6-2=4,
∵AE2=AB•EB,
∴AE:AB=
| ||
| 2 |
∴DQ:DH=
| ||
| 2 |
∵QF∥CH,
∴QF:HC=DQ:DH=
| ||
| 2 |
∴QF=
| ||
| 2 |
| 5 |
∴EF=EQ+QF=2
| 5 |
故答案为2
| 5 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.也考查了平行线分线段成比例定理.
| ||
| 2 |

练习册系列答案
相关题目
在代数式:a,
(a+b)h,3.14k2,
,
,
,中,单项式的个数为( )
| 1 |
| 2 |
| 1 |
| a |
| 3x-1 |
| 2 |
| 1 |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
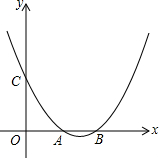 已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧.
已知二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,若点A的坐标是(1,0),点B在点A的右侧. 如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.
如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.