题目内容
某商店购进800个旅游纪念品,进价为每个50元,第一周以每个80元的价格售出200个,第二周若按每个80元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出10个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品以及清仓处理,以每个40元的价格全部售出,如果这批旅游纪念品共获利9000元.
(1)填表(结果需化简)
(2)求第二周每个旅游纪念品的销售价格为多少元?
(1)填表(结果需化简)
| 时间 | 第一周 | 第二周 | 清仓时 |
| 单价(元) | 80 | 40 | |
| 销售量(件) | 200 |
考点:一元二次方程的应用
专题:销售问题
分析:(1)第二周的单价=第一周的单价-降低的价格,销售量=200+10×降低的单价;清仓时的销售量为:800-第一周的销售量-第二周的销售量;
(2)等量关系为:总售价-总进价=9000.把相关数值代入计算即可.
(2)等量关系为:总售价-总进价=9000.把相关数值代入计算即可.
解答:解:
(1)
(2)80×200+(80-x)(200+10x)+40×[800-200-(200+10x)]-800×50=9000,
x2-20x+100=0,
解得:x1=x2=10,
当x=10时,80-x=70.
答:第二周每个旅游纪念品的销售价格为70元.
故答案为80-x,200+10x,400-10x.
(1)
| 时间 | 第一周 | 第二周 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+10x | 400-10x |
x2-20x+100=0,
解得:x1=x2=10,
当x=10时,80-x=70.
答:第二周每个旅游纪念品的销售价格为70元.
故答案为80-x,200+10x,400-10x.
点评:本题考查一元二次方程的应用;用列表格的方法得到第2周的单价和销售量以及清仓时的销售量是解决本题的突破点;得到总利润的等量关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
可以由抛物线y=x2平移得到抛物线y=(x-2)2+1,下列平移方法中正确的是( )
| A、向右平移2个单位,再向上平移1个单位 |
| B、向右平移2个单位,再向下平移1个单位 |
| C、向左平移2个单位,再向上平移1个单位 |
| D、向左平移2个单位,再向下平移1个单位 |
 如图,在菱形ABCD中,AB=5,∠ABC=120°,则对角线BD等于( )
如图,在菱形ABCD中,AB=5,∠ABC=120°,则对角线BD等于( )| A、20 | B、15 | C、10 | D、5 |
以2、4为两边长的三角形的第三边长是方程x2-7x+10=0的根,则这个三角形的周长为( )
| A、8 | B、11 |
| C、11或8 | D、以上都不对 |
下列一元二次方程用配方法解比较简单的是( )
| A、x2-x-5=0 |
| B、(x-2)2=5 |
| C、x2+4x-6=0 |
| D、x2-3x=0 |
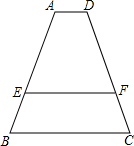 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=