题目内容
17．若x，y 为实数，且|y-1|+x2-2xy+y2=0，则x+y的值为2．分析 先将已知等式转化为|y-1|+（x-y）2=0的形式，然后根据非负数的性质得到y=1，x=y=1，然后求x+y的值．
解答 解：由|y-1|+x2-2xy+y2=0，得
|y-1|+（x-y）2=0，
所以到y=1，x=y=1，
所以x+y=1+1=2．
故答案是：2．
点评 本题考查了配方法的应用，非负数的性质．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
如图所示，已知∠DAC=∠ACB，∠D=62°，求∠BCD的度数．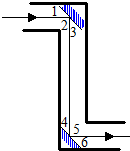
如图所示，潜望镜的两个镜子是平行放置的，光线经过镜子反射后，有∠1=∠3，∠4=∠6，请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的？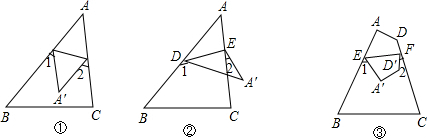
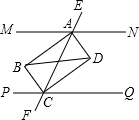已知MN∥PQ，同旁内角的平分线AB、BC和AD、CD分别相交于点B、D．
9．下列各式从左到右的变形中，属于因式分解的是（ ）
| A． | ${x^2}+3x-4=x（{x+3-\frac{4}{x}}）$ | B． | （x+2）（x-2）=x2-4 | ||
| C． | x2-4+3x=（x+2）（x-2）+3x | D． | $-{x^2}+x-\frac{1}{4}=-{（{x-\frac{1}{2}}）^2}$ |
如图，在平面直角坐标系xoy中，已知点A（2，1）、B（-1，1）、C（-1，-3）、D（2，-3），把一根长为2015个单位长度没有弹性的细线（线的粗细忽略不计）的一端固定在D处，并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标为（2，-2）．
如图，在?ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．