题目内容
7. 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
分析 (1)根据平行四边形的性质可得AO=$\frac{1}{2}$AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
(2)根据相似三角形的性质可得GC=3AG,则有AC=4AG,从而可得AO=$\frac{1}{2}$AC=2AG,即可得到GO=AO-AG=AG;
(3)根据相似三角形的性质可得AG=$\frac{1}{4}$AC,AH=$\frac{2}{5}$AC,结合AO=$\frac{1}{2}$AC,即可得到a=$\frac{1}{4}$AC,b=$\frac{3}{20}$AC,c=$\frac{1}{10}$AC,就可得到a:b:c的值.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AO=$\frac{1}{2}$AC,AD=BC,AD∥BC,
∴△AEG∽△CBG,
∴$\frac{EG}{GB}$=$\frac{AG}{GC}$=$\frac{AE}{BC}$.
∵AE=EF=FD,
∴BC=AD=3AE,
∴GC=3AG,GB=3EG,
∴EG:BG=1:3;
(2)∵GC=3AG(已证),
∴AC=4AG,
∴AO=$\frac{1}{2}$AC=2AG,
∴GO=AO-AG=AG;
(3)∵AE=EF=FD,
∴BC=AD=3AE,AF=2AE.
∵AD∥BC,
∴△AFH∽△CBH,
∴$\frac{AH}{HC}$=$\frac{AF}{BC}$=$\frac{2AE}{3AE}$=$\frac{2}{3}$,
∴$\frac{AH}{AC}$=$\frac{2}{5}$,即AH=$\frac{2}{5}$AC.
∵AC=4AG,
∴a=AG=$\frac{1}{4}$AC,
b=AH-AG=$\frac{2}{5}$AC-$\frac{1}{4}$AC=$\frac{3}{20}$AC,
c=AO-AH=$\frac{1}{2}$AC-$\frac{2}{5}$AC=$\frac{1}{10}$AC,
∴a:b:c=$\frac{1}{4}$:$\frac{3}{20}$:$\frac{1}{10}$=5:3:2.
点评 本题主要考查了相似三角形的判定与性质、平行四边形的性质、合比性质等知识,由两直线平行联想到三角形相似,从而得到边成比例,是常用的一种方法,应熟练掌握.

| 物体重 质量(g) | 100 | 200 | 300 | 400 | 500 |
| 弹簧长 (cm) | 20 | 22 | 24 | 26 | 28 |
(2)写出弹簧长度y(cm)与所挂物体重量x(g)之间的函数关系式;
(3)当x=650g时,y的值是多少?
| 届数 | 第13届 | 第14届 | 第15届 | 第16届 |
| 金牌数(枚) | 129 | 150 | 168 | 198 |
| 银牌数(枚) | 77 | 84 | 88 | 118 |
中国体育代表团第13-16届亚运会上获得金银牌情况统计图.

(2)第16届广州亚运会上,中国代表团获得的金牌数比第14届韩国釜山获得的金牌数多百分之几?
(3)请你对我国体育代表团在第16届广州亚运会获得的成绩做简单的评价.
 如图,在△ABC中,AB=4,AD是△ABC的平分线,DE⊥AB于E,且DE=2
如图,在△ABC中,AB=4,AD是△ABC的平分线,DE⊥AB于E,且DE=2
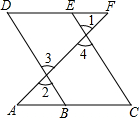 如图,E点为DF上的点,B为AC上的点,如果∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.
如图,E点为DF上的点,B为AC上的点,如果∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.