题目内容
12．
在我市开展的“美丽山城，创卫我同行”活动中，某校倡议八年级学生利用双休日在各自社区参加义务劳动．为了解同学们劳动情况，学校随机调查了部分同学的劳动时间，并用得到的数据绘制成不完整的统计图表，如图所示：| 劳动时间（时） | 频数（人数） | 频率 |
| 0.5 | 12 | 0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
（2）请将统计图补充完整；
（3）请你估计如果有2000名学生参加义务劳动时间超过1小时的人数．
分析 （1）参加义务劳动的时间为0.5小时的同学数除以它所占的百分比可得m的值，然后用m的值乘以0.4得到x的值，同18除以m的值得y的值；
（2）利用x=40将频数分布直方图补充完整；
（3）根据公式求解．
解答 解：（1）m=12÷0.12=100，x=100×0.4=40，y=18÷100=0.18；
故答案为100，40，0.18；
（2）如图，
（3）2000名学生参加义务劳动时间超过1小时的人数2000×（0.4+0.18）=1160人．
点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．也考查了统计图．
练习册系列答案
相关题目
2．
二次函数y1=a（x-2）2的图象与直线交于A（0，-1），B（2，0）两点．
（1）确定二次函数y1与直线AB的解析式y2；
（2）根据图象，分别确定当y1＜y2，y1=y2时，自变量x的取值范围．
二次函数y1=a（x-2）2的图象与直线交于A（0，-1），B（2，0）两点．（1）确定二次函数y1与直线AB的解析式y2；
（2）根据图象，分别确定当y1＜y2，y1=y2时，自变量x的取值范围．
20．
某校为了了解该校初二年级学生阅读课外书籍的情况，随机抽取了该年级的部分学生，对他们某月阅读课外书籍的情况进行了调查，并根据调查的结果绘制了如图的统计图表．
表1 阅读课外书籍人数分组统计表
请你根据以上信息解答下列问题：
（1）这次共调查了学生多少人？
（2）E组人数在这次调查中所占的百分比是多少？
（3）求出表1中a的值，并补全图1；
（4）若该年级共有学生300人，请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人？
某校为了了解该校初二年级学生阅读课外书籍的情况，随机抽取了该年级的部分学生，对他们某月阅读课外书籍的情况进行了调查，并根据调查的结果绘制了如图的统计图表．表1 阅读课外书籍人数分组统计表
| 分组 | 阅读课外书籍时间n（小时） | 人数 |
| A | 0≤n＜3 | 3 |
| B | 3≤n＜6 | 10 |
| C | 6≤n＜9 | a |
| D | 9≤n＜12 | 13 |
| E | 12≤n＜15 | b |
| F | 15≤n＜18 | c |
（1）这次共调查了学生多少人？
（2）E组人数在这次调查中所占的百分比是多少？
（3）求出表1中a的值，并补全图1；
（4）若该年级共有学生300人，请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人？
（1）阅读理解：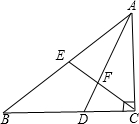
如图，△ABC中，∠ACB=90°，D在BC上，E为AB之中点，AD、CE相交于F，且AD=DB．若∠B=35°，求∠DFE的度数．
已知线段b和∠α，用尺规作一个三角形，使它的两边长分别为b和2b，且这两条边的夹角等于∠α．（不写作法，保留作图痕迹）