题目内容
8.将分式$\frac{3x-7}{{x}^{2}-3x-4}$拆分成两个分式和的形式时,可设待定系数A、B,使$\frac{3x-7}{{x}^{2}-3x-4}$=$\frac{A}{x-4}+\frac{B}{x+1}$,则A=1,B=2.分析 已知等式右边通分并利用同分母分式的加法法则计算,利用分式相等的条件求出A与B的值即可.
解答 解:$\frac{3x-7}{(x-4)(x+1)}$=$\frac{A}{x-4}$+$\frac{B}{x+1}$=$\frac{A(x+1)+B(x-4)}{(x-4)(x+1)}$,
可得3x-7=(A+B)x+A-4B,
∴$\left\{\begin{array}{l}{A+B=3}\\{A-4B=-7}\end{array}\right.$,
解得:A=1,B=2.
故答案为:1;2.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.当x=-3时,分式$\frac{{x}^{2}-9}{x-3}$的值为0;若$\frac{x-y}{y}$=$\frac{1}{2}$,则$\frac{x}{y}$=$\frac{3}{2}$.
13.下列计算正确的是( )
| A. | a6÷a2=a3 | B. | (a2)3=a5 | C. | $\sqrt{16}$=±4 | D. | $\root{3}{-8}$=-2 |
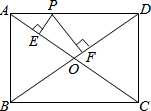 矩形ABCD中,AB=3,AD=4;P是AD上的任意一点,过P作PE⊥OA,PF⊥OD,求PE+PF的值?
矩形ABCD中,AB=3,AD=4;P是AD上的任意一点,过P作PE⊥OA,PF⊥OD,求PE+PF的值?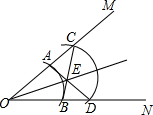 有位同学发现了“角平分线”的另一种尺规作法,其方法为:
有位同学发现了“角平分线”的另一种尺规作法,其方法为: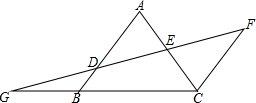 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=EF,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=EF,分别延长FD和CB交于点G.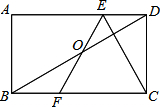 如图,矩形ABCD中,E、F分别是AD、BC上的点,且DE=BF,EF与BD交于点O.
如图,矩形ABCD中,E、F分别是AD、BC上的点,且DE=BF,EF与BD交于点O. 如图,一点光源在(0,3)处,沿所示的方向发射,长方形四条边上有四个平面镜,与坐标平面垂直放置,设第一个入射点P1坐标为(3,0),则第二个入射点P2(6,3),第三个入射点P3(3,6),作出光路图,并写出第2013个入射点P2013(3,0)
如图,一点光源在(0,3)处,沿所示的方向发射,长方形四条边上有四个平面镜,与坐标平面垂直放置,设第一个入射点P1坐标为(3,0),则第二个入射点P2(6,3),第三个入射点P3(3,6),作出光路图,并写出第2013个入射点P2013(3,0)