题目内容
16.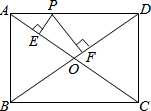 矩形ABCD中,AB=3,AD=4;P是AD上的任意一点,过P作PE⊥OA,PF⊥OD,求PE+PF的值?
矩形ABCD中,AB=3,AD=4;P是AD上的任意一点,过P作PE⊥OA,PF⊥OD,求PE+PF的值?
分析 连接OP,由矩形ABCD的性质得出OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,∠BAD=90°,由勾股定理求出BD,得出OA=OD=$\frac{5}{2}$,S△AOD=$\frac{1}{4}$S矩形ABCD=3,然后由S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA(PE+PF),即可得出结果.
解答 解:连接OP,
∵四边形ABCD是矩形,AB=3,BC=4,
∴S矩形ABCD=AB•BC=12,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5,S△AOD=$\frac{1}{4}$S矩形ABCD=$\frac{1}{4}$×4×3=3,
∴OA=OD=$\frac{5}{2}$,
∴S△AOD=S△AOP+S△DOP=$\frac{1}{2}$OA•PE+$\frac{1}{2}$OD•PF=$\frac{1}{2}$OA(PE+PF)=$\frac{1}{2}$×$\frac{5}{2}$×(PE+PF)=3,
∴PE+PF=$\frac{12}{5}$.
点评 本题考查了矩形的性质、勾股定理、矩形的面积以及三角形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
7.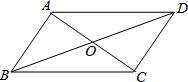 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )| A. | ∠BAD=∠BCD,∠ABC=∠ADC | B. | OA=OC,OB=OD | ||
| C. | AD∥BC,AB=CD | D. | AC=BD,AD=CD |
4.-32的相反数是( )
| A. | 9 | B. | -9 | C. | 6 | D. | -6 |
1.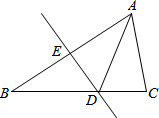 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
 如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )
如图,DE为AB边的垂直平分线,若△ACD的周长为7cm,若△ABC的周长为12cm,则AB长为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
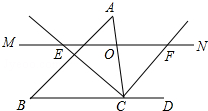 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.
如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.