题目内容
19.当x=-3时,分式$\frac{{x}^{2}-9}{x-3}$的值为0;若$\frac{x-y}{y}$=$\frac{1}{2}$,则$\frac{x}{y}$=$\frac{3}{2}$.分析 根据分式的值为零的条件以及分式无意义的条件即可求出x的值;先得出x与y的关系,再代入即可.
解答 解:因为分式$\frac{{x}^{2}-9}{x-3}$的值为0,可得:x-3≠0,x2-9=0,
可得:x=-3;
因为$\frac{x-y}{y}$=$\frac{1}{2}$,可得:y=2x-2y,
可得:2x=3y,
则$\frac{x}{y}$=$\frac{3}{2}$,
故答案为:=-3;$\frac{3}{2}$
点评 此题考查分式的值为零问题,若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可,分式无意义,分母为0.

练习册系列答案
相关题目
7.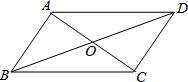 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
 如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )
如图,已知?ABCD中,对角线AC与BD相交于点O,下列结论错误的是( )| A. | ∠BAD=∠BCD,∠ABC=∠ADC | B. | OA=OC,OB=OD | ||
| C. | AD∥BC,AB=CD | D. | AC=BD,AD=CD |
14.抛物线y=(x+4)2+3的顶点坐标是( )
| A. | (4,-3) | B. | (-4,-3) | C. | (4,3) | D. | (-4,3) |
4.-32的相反数是( )
| A. | 9 | B. | -9 | C. | 6 | D. | -6 |
 如图,已知:∠A=∠C,DF平分∠CDO,BE平分∠ABO,DF与BE平行吗?试说明理由.
如图,已知:∠A=∠C,DF平分∠CDO,BE平分∠ABO,DF与BE平行吗?试说明理由.