题目内容
15.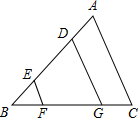 如图,在△ABC中,AD=BE,EF∥DG∥AC.
如图,在△ABC中,AD=BE,EF∥DG∥AC.(1)求证:BF=GC;
(2)判断EF,DG,AC三条线段之间的数量关系,并证明.
分析 (1)根据平行线分线段成比例定理证明;
(2)作△ABC的中位线PQ交AB于P,交BC于Q,根据三角形中位线定理和梯形的中位线定理证明即可.
解答 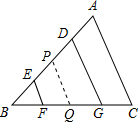 证明:(1)∵EF∥DG∥AC,
证明:(1)∵EF∥DG∥AC,
∴$\frac{BE}{AD}=\frac{BF}{GC}$,又AD=BE,
∴BF=GC;
(2)EF+DG=AC.
理由如下:作△ABC的中位线PQ交AB于P,交BC于Q,
则PQ=$\frac{1}{2}$AC,
∵BP=PA,BE=AD,
∴EP=PD,
同理FQ=QG,
∴PQ=$\frac{1}{2}$(EF+DG),
∴EF+DG=AC.
点评 本题考查的是三角形中位线定理和梯形的中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半;梯形的中位线平行于两底,并且等于两底和的一半.

练习册系列答案
相关题目
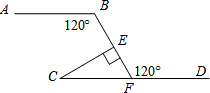 已知:如图,AB∥CD,∠ABF=120°,CE⊥BF,垂足为E,则∠ECF=30°.
已知:如图,AB∥CD,∠ABF=120°,CE⊥BF,垂足为E,则∠ECF=30°.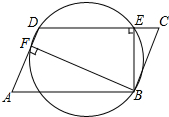 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.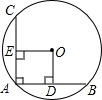 如图,在⊙O中,AB⊥AC,且AB=AC,0E⊥AC,0D⊥AB,且点E,D为垂足,四边形ADOE是正方形吗?请说明理由.
如图,在⊙O中,AB⊥AC,且AB=AC,0E⊥AC,0D⊥AB,且点E,D为垂足,四边形ADOE是正方形吗?请说明理由.