题目内容
4.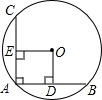 如图,在⊙O中,AB⊥AC,且AB=AC,0E⊥AC,0D⊥AB,且点E,D为垂足,四边形ADOE是正方形吗?请说明理由.
如图,在⊙O中,AB⊥AC,且AB=AC,0E⊥AC,0D⊥AB,且点E,D为垂足,四边形ADOE是正方形吗?请说明理由.
分析 先根据垂径定理,由OD⊥AB,OE⊥AC得到AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,且∠ADO=∠AEO=90°,加上∠DAE=90°,则可判断四边形ADOE是矩形,由于AB=AC,所以AD=AE,于是可判断四边形ADOE是正方形.
解答 解:是正方形,理由如下:
∵OD⊥AB于D,OE⊥AC于E,
∵AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,∠ADO=∠AEO=90°,
∵AB⊥AC,
∴∠DAE=90°,
∴四边形ADOE是矩形,
∵AB=AC,
∴AD=AE,
∴四边形ADOE是正方形.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了正方形的判定.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
13.已知:P($\frac{3m-2}{5}$,$\frac{m+1}{3}$)点在y轴上,则P点的坐标为( )
| A. | (0,-$\frac{5}{9}$) | B. | ($\frac{7}{9}$,0) | C. | (0,$\frac{5}{9}$) | D. | (-$\frac{5}{9}$,0) |
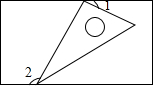 如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.
如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.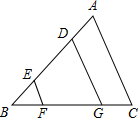 如图,在△ABC中,AD=BE,EF∥DG∥AC.
如图,在△ABC中,AD=BE,EF∥DG∥AC.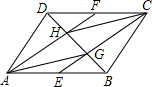 如图,ABCD为平行四边形,E、F分别为AB、CD的中点.
如图,ABCD为平行四边形,E、F分别为AB、CD的中点.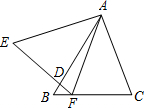 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论: