题目内容
8.在平行四边形ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,则平行四边形ABCD的周长等于12或20.分析 根据题意分别画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
解答 解:如图1所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,AB=CD=5,
BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∴AD=BC=5,
∴?ABCD的周长等于:20,
如图2所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,AB=CD=5,
BE=3,
∴BC=3-2=1,
∴?ABCD的周长等于:1+1+5+5=12,
则?ABCD的周长等于12或20.
故答案为:12或20.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.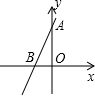 如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
 如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )
如图,直线y=kx+b经过点A(0,4),点B(-2,0),不等式0<kx+b<4的解集是( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
16.A、B两个水果市场各有荔枝13吨,现从A、B向甲、乙两地运送荔枝,其中甲地需要荔枝14吨,乙地需要荔枝12吨,从A到甲地的运费为50元/吨,到乙地的运费为30元/吨,从B到甲地的运费为60元/吨,到乙地的运费为45元/吨.
(1)设A地到甲地运送荔枝x吨,请完成下表:
(2)设总运费为W元,请写出W与x的函数关系式,并直接写出x的取值范围.
(3)怎样调送荔枝才能使运费最少?
(1)设A地到甲地运送荔枝x吨,请完成下表:
| 调往甲地(单位:吨) | 调往乙地(单位:吨) | |
| A | x | 13-x |
| B | 14-x | x-1 |
(3)怎样调送荔枝才能使运费最少?
20.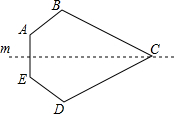 如图:如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=100°,则∠BCD的度数为( )
如图:如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=100°,则∠BCD的度数为( )
 如图:如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=100°,则∠BCD的度数为( )
如图:如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=100°,则∠BCD的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 90° |
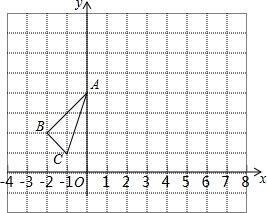 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点:
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点: