题目内容
4.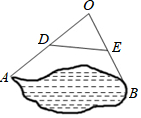 如图,为测量池塘边上两点A,B之间的距离,可以在池塘的一侧选取一点O,连接OA,OB,并分别取它们的中点D,E,连接DE,现测出AO=36米,BO=30米,DE=20米,那么A,B间的距离是( )
如图,为测量池塘边上两点A,B之间的距离,可以在池塘的一侧选取一点O,连接OA,OB,并分别取它们的中点D,E,连接DE,现测出AO=36米,BO=30米,DE=20米,那么A,B间的距离是( )| A. | 30米 | B. | 40米 | C. | 60米 | D. | 72米 |
分析 连接AB,可知DE为△OAB的中位线,由中位线定理可求得AB的长.
解答  解:
解:
如图,连接AB,
∵D、E分别为OA和OB的中点,
∴DE为△OAB的中位线,
∴AB=2DE=40米,
故选B.
点评 本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.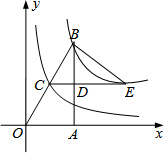 如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
 如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )
如图,在Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C、D分别是BO、BA的中点,点E在CD的延长线上.若函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过B,E,函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象经过点C,且△BCE的面积为1,则k2的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 与k1的值有关 |
16.若关于x,y的二元一次方程组$\left\{\begin{array}{l}2x+y=3k-1\\ x+2y=-2\end{array}\right.$的解满足x+y=1,则k=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
17. 如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
 如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )| A. | AB∥DF | B. | ∠B=∠E | ||
| C. | AB=DE | D. | AD的连线被MN垂直平分 |
 已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程)
已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程) 如图,六边形ABCDEF是正六边形,那么∠α的度数是60°.
如图,六边形ABCDEF是正六边形,那么∠α的度数是60°.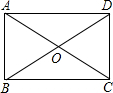 如图,矩形ABCD的对角线AC,BD交于点O,AB=2,∠AOB=60°,则BD的长为4.
如图,矩形ABCD的对角线AC,BD交于点O,AB=2,∠AOB=60°,则BD的长为4.