题目内容

16．若关于x，y的二元一次方程组$\left\{\begin{array}{l}2x+y=3k-1\\ x+2y=-2\end{array}\right.$的解满足x+y=1，则k=（　　）
A．-1B．1C．2D．3

分析 方程组两方程相加表示出x+y，代入x+y=1中计算即可求出k的值．

解答 解：$\left\{\begin{array}{l}{2x+y=3k-1①}\\{x+2y=-2②}\end{array}\right.$，
①+②得：3（x+y）=3k-3，即x+y=k-1，
代入x+y=1中得：k-1=1，
解得：k=2，
故选C

点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．

练习册系列答案
相关题目
3．已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．
（1）当∠MBN绕B点旋转到AE=CF时（如图1），若AE=1，试求AB的长；
（2）当∠MBN绕B点旋转到AE≠CF时，在图2这种情况下，求证AE+CF=EF；
（3）当∠MBN绕B点旋转到AE≠CF时，在图3这种情况下，（2）中结论是否成立？若成立，请给予证明；若不成立，线段AE、CF、EF又有怎样的数量关系？请直接写出你的猜想．
4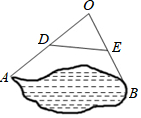．如图，为测量池塘边上两点A，B之间的距离，可以在池塘的一侧选取一点O，连接OA，OB，并分别取它们的中点D，E，连接DE，现测出AO=36米，BO=30米，DE=20米，那么A，B间的距离是（　　）
A．30米B．40米C．60米D．72米
4．如图，按此规律，第30行最后一个数是88．
11．将分式：$\frac{{x}^{2}-3x+2}{{x}^{2}+x-6}×[\frac{1}{x+3}]^{-1}$化简的结果是x-1．
1．下列计算正确的是（　　）
A．（a4）3=a7B．a8÷a4=a2C．（ab）3=a3b3D．（a+b）2=a2+b2
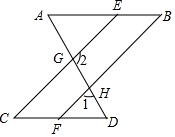8．如图，已知∠A=∠AGE，∠D=∠DGC．
（1）求证：AB∥CD；
（2）若∠2+∠1=180°，且∠BEC=2∠B+30°，求∠B的度数．
6．在等边△ABC中，点D是线段BC的中点，∠EDF=120°，线段DE与线段AB相交于点E．线段DF与线段AC相交于点F．
（1）如图一，若DF⊥AC，请直接写出DE与AB的位置关系；
（2）请判断DE与DF的数量关系．并写出推理过程．
（3）如图二，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．（2）中的结论还成立吗？若成立，写出证明过程，若不成立，说明理由．
（4）在∠EDF绕点D顺时针旋转过程中，直接用等式表示线段BE、CF、AB之间的数量关系．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网