题目内容
2. 星期日,小英与小平同时从家里出发返回学校,速度分别为3千米/小时,4千米/小时,小平家离学校18千米,小英家在小平返校的路上,离小平家2千米.
星期日,小英与小平同时从家里出发返回学校,速度分别为3千米/小时,4千米/小时,小平家离学校18千米,小英家在小平返校的路上,离小平家2千米.(1)分别写出小英、小平离小平家的距离y(千米)与行走时间t(小时)的函数关系式;
(2)在同一直角坐标系中画出上述两个函数的图象;
(3)返校路上,小平能否追上小英?如能,出发后几小时追上?
(4)从图象上看:谁先到达学校?
分析 (1)根据距离=2+速度×时间,即可找出小英离小平家的距离y1(千米)与行走时间t(小时)的函数关系式,根据距离=速度×时间,即可找出小平离小平家的距离y2(千米)与行走时间t(小时)的函数关系式;
(2)画出两函数图象,如图所示;
(3)观察函数图象,可知小平能追上小英,令4x=3x+2,求出x值即可;
(4)观察函数图象,由小平到校需要时间短,即可得出结论.
解答 解:(1)根据题意得:小英离小平家的距离y1(千米)与行走时间t(小时)的函数关系式为y1=3x+2(0≤x≤$\frac{16}{3}$);
小平离小平家的距离y2(千米)与行走时间t(小时)的函数关系式为y2=4x(0≤x≤$\frac{9}{2}$).
(2)当x=0时,y小英=3x+2=2;
当x=5时,y小英=3x+2=17;
当x=0时,y小平=4x=0;
当x=4时,y小平=4x=16.
画出上述两个函数的图象,如图所示.
(3)观察函数图象可知,小平能追上小英,
令4x=3x+2,解得:x=2,
∴小平出发2小时后追上小英.
(4)观察函数图象,可知小平先到达学校.
点评 本题考查了一次函数的应用、一次函数图象上点的坐标特征、一次函数的图象以及解一元一次方程,解题的关键是:(1)根据数量关系列出函数关系式;(2)画出两函数图象;(3)令4x=3x+2,求出x值;(4)观察函数图象,找出谁先到校.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.化化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;这种C产品中A的含量不能低于10%,又不能高于60%;C产品的出厂价经核算是含B的质量的一次函数.经市场调查,当含A的质量不高于8kg时:利润=出厂价-成本;当含A的质量不低于8kg时,每个C产品的利润将与含A的质量成反比例.
下表是每个C产品的成本及出厂价一览表的一部分.
(1)求出每个C产品的成本y(元)与含A的质量x(kg)之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用);
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
下表是每个C产品的成本及出厂价一览表的一部分.
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
10.若$\frac{3-2x}{x-1}$= +$\frac{1}{x-1}$,则 中的数是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 任意实数 |
17.今年5月21日是全国第27个助残日,某地开展“心手相连,共浴阳光”为主题的手工制品义卖销售活动.长江特殊教育学校将同学们手工制作的手串、中国结、手提包、木雕笔筒的相关销售信息汇总如下表,其中销售率最高的是( )
| 手工制品 | 手串 | 中国结 | 手提包 | 木雕笔筒 |
| 总数量(个) | 200 | 100 | 80 | 70 |
| 销售数量(个) | 190 | 100 | 76 | 68 |
| A. | 手串 | B. | 中国结 | C. | 手提包 | D. | 木雕笔筒 |
11.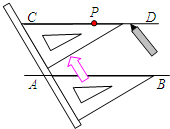 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线品行 | |
| D. | 过直线外一点有且只有一条直线与这条直线平行 |
12.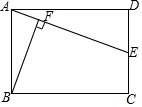 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )| A. | $\frac{3\sqrt{10}}{2}$ | B. | $\frac{3\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
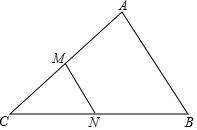 如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.
如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.