题目内容
11.①$\frac{1}{x-1}-\frac{3}{x+1}=\frac{x+3}{{{x^2}-1}}$;②$\frac{x}{x-2}-\frac{1}{{{x^2}-4}}=1$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:①去分母得:x+1-3x+3=x+3,
移项合并得:3x=1,
解得:x=$\frac{1}{3}$,
经检验x=$\frac{1}{3}$是分式方程的解;
②去分母得:x(x+2)-1=x2-4,
解得:x=-$\frac{3}{2}$,
经检验x=-$\frac{3}{2}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
2.已知关于x、y的不等式组$\left\{{\begin{array}{l}{x+2y=1+m}\\{2x+y=2}\end{array}}\right.$,若其中的未知数x、y满足x+y>0,则m的取值范围是( )
| A. | m>-4 | B. | m>-3 | C. | m<-4 | D. | m<-3 |
3.圆柱的侧面展开图不可能是( )
| A. | 平行四边形 | B. | 正方形 | C. | 矩形 | D. | 梯形 |
1.下列图形中,既是轴对称图形又是中心对称图形的是:( )
| A. |  | B. |  | C. |  | D. |  |
 如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
如图,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.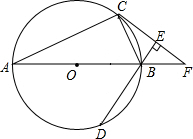 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB,垂足为点E,直线AB与CE交于点F.
如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB,垂足为点E,直线AB与CE交于点F.