题目内容
1.等边△ABC的三条边上,有三条相等的线段A1A2、B1B2、C1C2.证明:直线B2C1、C2A1、A2B1所成的三角形上三条线段B2C1、C2A1、A2B1与包含它们的边成比例.分析 由这六个点为△ABC三边的三等分点,可得出三对相似三角形:△AB2C1∽△ABC,△BA1C2∽△BCA,△CA2B1∽△CBA;再由相似三角形的性质可得$\frac{{B}_{2}{C}_{1}}{BC}$=$\frac{{A}_{1}{A}_{2}}{BC}$=$\frac{1}{3}$,$\frac{{A}_{1}{C}_{2}}{AC}$=$\frac{{B}_{1}{B}_{2}}{AC}$=$\frac{1}{3}$,$\frac{{A}_{2}{B}_{1}}{AB}$=$\frac{{C}_{1}{C}_{2}}{AB}$=$\frac{1}{3}$.
解答 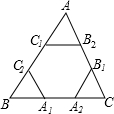 解:∵等边△ABC的三条边上,有三条相等的线段A1A2、B1B2、C1C2,
解:∵等边△ABC的三条边上,有三条相等的线段A1A2、B1B2、C1C2,
∴A1、A2、B1、B2、C1、C2为△ABC三边的三等分点,
∴B2C1∥BC,A1C2∥AC,A2B1∥AB,
∴△AB2C1∽△ABC,△BA1C2∽△BCA,△CA2B1∽△CBA,
∴$\frac{{B}_{2}{C}_{1}}{BC}$=$\frac{{A}_{1}{A}_{2}}{BC}$=$\frac{1}{3}$,$\frac{{A}_{1}{C}_{2}}{AC}$=$\frac{{B}_{1}{B}_{2}}{AC}$=$\frac{1}{3}$,$\frac{{A}_{2}{B}_{1}}{AB}$=$\frac{{C}_{1}{C}_{2}}{AB}$=$\frac{1}{3}$.
点评 本题考查了相似三角形的判定与性质,等边三角形的判定与性质.根据题意推知B2C1∥BC,A1C2∥AC,A2B1∥AB是解题的难点.

练习册系列答案
相关题目
17.若a满足|2015-a|+$\sqrt{a-2016}$=a,则20152-a的值为( )
| A. | 2015 | B. | -2015 | C. | 2016 | D. | -2016 |
14.在下列表示的不等式的解集中,不包括-5的是( )
| A. | x≤4 | B. | x≥-5 | C. | x≤-6 | D. | x≥-7 |
10. 如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
 如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )| A. | 3 | B. | 5$\sqrt{2}$-3 | C. | 4 | D. | 5 |
 已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.
已知如图,在梯形ABCD中AB∥CD,对角线AC、BD交于点O,△ABC为边长为6的等边三角形,DC=2.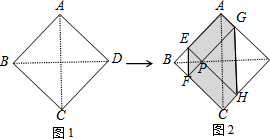 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断: