题目内容
4.关于x的方程x2-2(k-1)x+k2=0有两个不相等的实根x1、x2,且有x1+x2=6-x1x2,则k的值是-4.分析 先根据判别式的意义可确定k<$\frac{1}{2}$,再根据根与系数的关系得到x1+x2=2(k-1),x1x2=k2,由于x1+x2=6-x1x2,则2(k-1)=6-k2,然后解此方程后利用k的取值范围确定满足条件的k的值.
解答 解:根据题意得△=4(k-1)2-4k2>0,
解得k<$\frac{1}{2}$,
而x1+x2=2(k-1),x1x2=k2,x1+x2=6-x1x2,
所以2(k-1)=6-k2,
整理得k2+2k-8=0,解得k1=-4,k2=2,
而k<$\frac{1}{2}$,
所以k的值为-4.
故答案为-4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
12.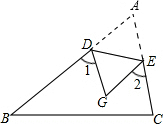 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
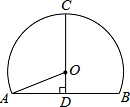 如图是一个单心圆隧道的截面,若路面AB宽为10m,高CD为7m,则此隧道单心圆的半径OA是$\frac{37}{7}$m.
如图是一个单心圆隧道的截面,若路面AB宽为10m,高CD为7m,则此隧道单心圆的半径OA是$\frac{37}{7}$m. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长. 甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.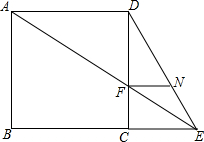 已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.
已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.