题目内容
14.二次函数y=ax2+bx+c(a≠0)自变量x与函数y的对应值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | m-4$\frac{1}{2}$ | m-2 | m-$\frac{1}{2}$ | m | m-$\frac{1}{2}$ | m-4$\frac{1}{2}$ | m-2 | m-4$\frac{1}{2}$ |
分析 根据函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根,再根据函数的增减性即可判断方程ax2+bx+c=0两个根的范围.
解答 解:∵1<m<1$\frac{1}{2}$,
∴-1<m-2<-$\frac{1}{2}$,$\frac{1}{2}$<m-$\frac{1}{2}$<1,
∴函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0.
由表中数据可知:y=0在y=m-2与y=m-$\frac{1}{2}$之间,
故对应的x的值在-1与0之间,即-1<x1<0,
y=0在y=m-2与y=m-$\frac{1}{2}$之间,故对应的x的值在2与3之间,即2<x2<3.
故答案为-1<x1<0,2<x2<3.
点评 此题主要考查了图象法求一元二次方程的近似值,掌握函数y=ax2+bx+c的图象与x轴的交点与方程ax2+bx+c=0的根的关系是解决此题的关键所在.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
4.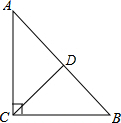 如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD是中线,若BC=6,AC=8,则tan∠ACD的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,△ABC中,AB的垂直平分线交AC与点M.若CM=4cm,BC=5cm,AM=6cm,则△MBC的周长=15cm.
如图,△ABC中,AB的垂直平分线交AC与点M.若CM=4cm,BC=5cm,AM=6cm,则△MBC的周长=15cm. 如图,在△ABD和△ACE中,有四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE,请你从其中三个等式作为题设,设另一个作为结论,写出一个真命题,并给出证明.(要求写出已知、求证及证明过程)
如图,在△ABD和△ACE中,有四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE,请你从其中三个等式作为题设,设另一个作为结论,写出一个真命题,并给出证明.(要求写出已知、求证及证明过程)