题目内容
3. 如图,在△ABD和△ACE中,有四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE,请你从其中三个等式作为题设,设另一个作为结论,写出一个真命题,并给出证明.(要求写出已知、求证及证明过程)
如图,在△ABD和△ACE中,有四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE,请你从其中三个等式作为题设,设另一个作为结论,写出一个真命题,并给出证明.(要求写出已知、求证及证明过程)
分析 此题无论选择什么作为题设,什么作为结论,它有一个相同点--都是通过证明△ABD≌△ACE,然后利用全等三角形的性质解决问题.
解答 解:解法一:如果AB=AC,AD=AE,BD=CE,那么∠1=∠2.
已知:在△ABD和△ACE中,AB=AC,AD=AE,BD=CE,
求证:∠1=∠2.
证明:在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠1=∠2.
解法二:如果AB=AC,AD=AE,∠1=∠2,那么BD=CE.
已知:在△ABD和△ACE中,AB=AC,AD=AE,∠1=∠2,
求证:BD=CE.
证明:∵∠1=∠2,
∴∠BAD=∠CAE.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE.
点评 此题考查全等三角形的判定和性质,熟练掌握判定方法是关键,全等三角形的判定方法有SSS、SAS、ASA、AAS、HL等.选择条件时要避开SSA与AAA.这两种不能作为三角形全等的判定方法加以应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
13.△ABC中,∠A:∠B:∠C=3:5:8,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形,且∠C=90° | ||
| C. | 直角三角形,且∠B=90° | D. | 直角三角形,且∠A=90° |
14.二次函数y=ax2+bx+c(a≠0)自变量x与函数y的对应值如下表:
若1<m<1$\frac{1}{2}$,则一元二次方程ax2+bx+c=0的两根x1,x2的取值范围是-1<x1<0,2<x2<3.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | m-4$\frac{1}{2}$ | m-2 | m-$\frac{1}{2}$ | m | m-$\frac{1}{2}$ | m-4$\frac{1}{2}$ | m-2 | m-4$\frac{1}{2}$ |
 实数a在数轴上的位置如图所示,则化简|a-2|+$\sqrt{{a}^{2}}$的结果为2.
实数a在数轴上的位置如图所示,则化简|a-2|+$\sqrt{{a}^{2}}$的结果为2.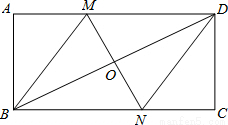 四边形ABCD是矩形,MN垂直平分对角线BD于O,交AD于M,交BC于N,求证:四边形MBND是菱形.
四边形ABCD是矩形,MN垂直平分对角线BD于O,交AD于M,交BC于N,求证:四边形MBND是菱形. 如图,平行四边形ABCD中,E是AB的中点,则$\frac{BE}{CD}$=$\frac{1}{2}$.
如图,平行四边形ABCD中,E是AB的中点,则$\frac{BE}{CD}$=$\frac{1}{2}$. 已知∠AOB,利用尺规作∠A1O1B1,使得∠AOB=2∠A1O1B1(要求不写作法,但要保留作图痕迹)
已知∠AOB,利用尺规作∠A1O1B1,使得∠AOB=2∠A1O1B1(要求不写作法,但要保留作图痕迹)