题目内容
4．
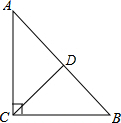如图，在Rt△ABC中，∠ACB=90°，CD是中线，若BC=6，AC=8，则tan∠ACD的值为（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 根据直角三角形斜边上的中线等于斜边的一半可得AD=CD，再根据等边对等角可得∠A=∠ACD，然后利用锐角的正切值等于对边比邻边列式计算即可得解．
解答 解：∵∠ACB=90°，CD是AB边上的中线，
∴AD=CD，
∴∠A=∠ACD，
∴tan∠ACD=tan∠A=$\frac{BC}{AC}$=$\frac{6}{8}$=$\frac{3}{4}$．
故选B．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，锐角三角函数的定义，熟记性质并求出∠A=∠ACD是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．二次函数y=ax2+bx+c（a≠0）自变量x与函数y的对应值如下表：
若1＜m＜1$\frac{1}{2}$，则一元二次方程ax2+bx+c=0的两根x1，x2的取值范围是-1＜x1＜0，2＜x2＜3．
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | m-4$\frac{1}{2}$ | m-2 | m-$\frac{1}{2}$ | m | m-$\frac{1}{2}$ | m-4$\frac{1}{2}$ | m-2 | m-4$\frac{1}{2}$ |
作图题：在图中画出△ABC关于直线l的轴对称图形△A1B1C1．
如图，⊙O是△ABC的外接圆，∠BOC=40°，则∠A的度数为20°．
已知∠AOB，利用尺规作∠A1O1B1，使得∠AOB=2∠A1O1B1（要求不写作法，但要保留作图痕迹）