题目内容
6.已知x是正整数,且满足y=$\frac{4}{x-1}$+$\sqrt{2-x}$,则x+y的平方根是±$\sqrt{6}$.分析 根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
解答 解:y=$\frac{4}{x-1}$+$\sqrt{2-x}$,
得$\left\{\begin{array}{l}{2-x≥0}\\{x-1≠0}\end{array}\right.$,
解得x=2,y=4,
x+y=2+4=6,
$±\sqrt{x+y}$=$±\sqrt{6}$.
故答案为:$±\sqrt{6}$.
点评 本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.单项式-23xy3的系数与次数分别是( )
| A. | -2,4 | B. | -8,4 | C. | -2,3 | D. | -6,3 |
14.二次函数y=ax2+bx+c(a≠0)自变量x与函数y的对应值如下表:
若1<m<1$\frac{1}{2}$,则一元二次方程ax2+bx+c=0的两根x1,x2的取值范围是-1<x1<0,2<x2<3.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | m-4$\frac{1}{2}$ | m-2 | m-$\frac{1}{2}$ | m | m-$\frac{1}{2}$ | m-4$\frac{1}{2}$ | m-2 | m-4$\frac{1}{2}$ |
 实数a在数轴上的位置如图所示,则化简|a-2|+$\sqrt{{a}^{2}}$的结果为2.
实数a在数轴上的位置如图所示,则化简|a-2|+$\sqrt{{a}^{2}}$的结果为2.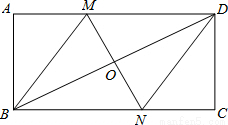 四边形ABCD是矩形,MN垂直平分对角线BD于O,交AD于M,交BC于N,求证:四边形MBND是菱形.
四边形ABCD是矩形,MN垂直平分对角线BD于O,交AD于M,交BC于N,求证:四边形MBND是菱形. 如图,⊙O是△ABC的外接圆,∠BOC=40°,则∠A的度数为20°.
如图,⊙O是△ABC的外接圆,∠BOC=40°,则∠A的度数为20°.