题目内容
11.(1)如图1,已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数;(2)如图2,已知射线Ox与射线Oy互相垂直,B,A分别为Ox、Oy上一动点,∠ABx、∠BAy的平分线交于C.问:B、A在Ox、Oy上运动过程中,∠C的度数是否改变?若不改变,求出其值;若改变,说明理由.
(3)如图3,E和D分别在△ABC的边BA和CA的延长线上,CF、EF分别平分∠ACB和∠AED,若∠B=70°,∠D=40°,求∠F的大小.
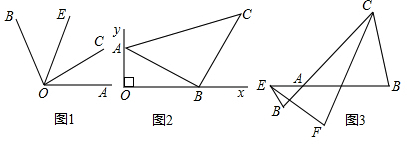
分析 (1)根据角平分线线的定义求得∠COB=80°.然后根据图中角与角间的和差关系得到∠AOB=∠AOC+∠COB=110°.
(2)根据三角形的内角和定理、角平分线定义和三角形的外角的性质可以得到∠C=90°-$\frac{1}{2}$∠O.
(3)由CF、EF分别平分∠ACB和∠AED,得∠3=∠4,∠1=∠2,所以有∠3+∠B=∠2+∠F;∠3+∠4+∠B=∠1+∠2+∠D,即2∠3+∠B=2∠2+∠D,而∠B=70°,∠D=40°,于是由两个等式即可求出∠F.
解答 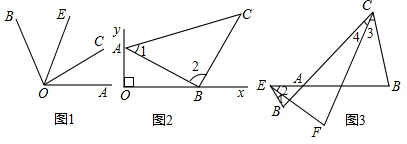 解:(1)如图1,∵OE是∠COB的平分线(已知),
解:(1)如图1,∵OE是∠COB的平分线(已知),
∴∠COB=2∠COE(角平分线定义),
∵∠COE=40°,
∴∠COB=80°.
∵∠AOC=30°,
∴∠AOB=∠AOC+∠COB=110°.
(2)如图2,∠C的度数不改变,为45°.
∵∠ABN、∠BAM的平分线交于C,
∴∠C=180°-(∠1+∠2)
=180°-$\frac{1}{2}$(∠ABN+∠BAM)
=180°-$\frac{1}{2}$(∠O+∠OAB+∠BAM)
=90°-$\frac{1}{2}$∠O
=45°.
(3)如图3,∵CF、EF分别平分∠ACB和∠AED,
∴∠3=∠4,∠1=∠2,
∵∠3+∠B=∠2+∠F;
∠3+∠4+∠B=∠1+∠2+∠D,即2∠3+∠B=2∠2+∠D,
又∵∠B=70°,∠D=40°,
∴∠3+70°=∠2+∠F①,
2∠3+70°=2∠2+40°②,
①×2-②得,70°=2∠F-40°,
解得∠F=55°.
点评 此题考查了三角形的内角和定理、三角形的外角的性质以及角平分线定义.根据题意得到∠C和∠O之间的数量关系(∠C=90°-$\frac{1}{2}$∠O)是解题的难点.

| A. | -3 | B. | 0 | C. | 1 | D. | -1 |
| A. | 向右平移2个单位 | B. | 向左平移2个单位 | C. | 向右平移4个单位 | D. | 向左平移4个单位 |
 浙江卫视六频道《我老爸最棒》栏目中有一项”“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为( )
浙江卫视六频道《我老爸最棒》栏目中有一项”“大力金刚”的游戏.如图,有6根柱子穿过了一堵木墙,蓝、绿两队的两位老爸分别站在木墙的左、右两侧,需把自己一侧的那段柱子推向对方侧.若每侧每段柱子被选中的机会相等,则两人选到同一根柱子的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{36}$ |




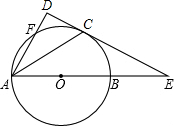 如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.