题目内容
13.学校组织的实践活动中,晓华同学用纸板制作了一个圆锥模型,它的底面直径为4,高为2$\sqrt{3}$,则这个圆锥的侧面积是( )| A. | 8π | B. | 16π | C. | 4$\sqrt{3}$π | D. | 8$\sqrt{7}$π |
分析 首先根据勾股定理计算出母线的长,再根据圆锥的侧面积为:S侧=$\frac{1}{2}$•2πr•l=πrl,代入数进行计算即可.
解答 解:∵底面直径为4,高为2$\sqrt{3}$,
∴母线长=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4.
底面圆的周长为:2π×4=8π.
∴圆锥的侧面积为:S侧=$\frac{1}{2}$•2πr•l=πrl=$\frac{1}{2}$×8π×2=8π.
故选A.
点评 此题主要考查了圆锥的计算,关键是掌握圆锥的侧面积公式:S侧=$\frac{1}{2}$•2πr•l=πrl.

练习册系列答案
相关题目
3.$\sqrt{3}$的相反数是( )
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
2.-3、0、1、-1四个数中,最小的数是( )
| A. | -3 | B. | 0 | C. | 1 | D. | -1 |
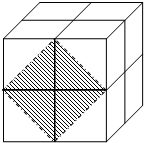 如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.
如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3. 如图,△ABC∽△DBA,若BD=2,DC=5,则AB=$\sqrt{14}$.
如图,△ABC∽△DBA,若BD=2,DC=5,则AB=$\sqrt{14}$.