题目内容
6. 如图,在?ABCD中,AD⊥BD,点E、F分别在AB、BD上且满足AD=AE=DF,连接DE、AF、EF.
如图,在?ABCD中,AD⊥BD,点E、F分别在AB、BD上且满足AD=AE=DF,连接DE、AF、EF.(1)若∠CDB=30°,求∠EAF的度数;
(2)若DE⊥EF,求证:DE=2EF.
分析 (1)利用平行线的性质以及等腰直角三角形的性质进而得出∠EAF的度数;
(2)首先过点A作AG⊥DE于点G,再利用全等三角形的判定与性质得出△FED≌△DGA,即可得出DG=EG=EF即可得出答案.
解答 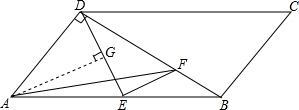 解:(1)∵在?ABCD中,CD∥AB,
解:(1)∵在?ABCD中,CD∥AB,
∴∠CDB=∠ABD=30°,
∵∠ADB=90°,
∴∠DAB=60°,
∵AD=DF,∠ADF=90°,
∴∠DAF=∠DFA=45°,
∴∠EAF=60°-45°=15°;
(2)证明:过点A作AG⊥DE于点G,
∵∠FDE+∠ADE=90°,∠DAG+∠ADG=90°,
∴∠FDE=∠DAG,
在△FED和△DGA中
∵$\left\{\begin{array}{l}{∠FED=∠DGA}\\{∠EDF=∠DAG}\\{DF=AD}\end{array}\right.$,
∴△FED≌△DGA(AAS),
∴DG=EF,
∵AD=AE,AG⊥DE,
∴DG=GE,
∴DG=EG=EF,
∴ED=2EF.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形的性质,得出△FED≌△DGA是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.射击队对甲、乙两名运动员进行了六次测试,测试成绩如下表(单位:环):
分别计算甲、乙六次测试成绩的方差.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 |
17.计算$\frac{\sqrt{8}}{\sqrt{12}}÷\sqrt{\frac{45}{12}}×\sqrt{\frac{5}{8}}$的值是( )
| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{3\sqrt{3}}{4}$ |
18.如图,∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |