题目内容
 如图,已知B是EC的中点,∠ABE=∠DBC,∠A=∠D,求证:DE=AC.
如图,已知B是EC的中点,∠ABE=∠DBC,∠A=∠D,求证:DE=AC.考点:全等三角形的判定与性质
专题:证明题
分析:根据线段中点的定义可得BE=BC,再根据等角的补角相等求出∠ABC=∠DBE,然后利用“角角边”证明△ABC和△DBE全等,根据全等三角形对应边相等证明即可.
解答:证明:∵B是EC的中点,
∴BE=BC,
∵∠ABE=∠DBC,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(AAS),
∴DE=AC.
∴BE=BC,
∵∠ABE=∠DBC,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
|
∴△ABC≌△DBE(AAS),
∴DE=AC.
点评:本题考查了全等三角形的判定与性质,等角的补角相等的性质,熟练掌握三角形全等的判断方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把多项式2xn+2+4xn-6xn-2分解因式,其结果应是( )
| A、2xn(x2+2-3x)=2xn(x-1)(x-2) |
| B、2xn-2(x2-3x+2)=2xn-2(x-1)(x-2) |
| C、2xn-2(x4+2x2-3)=2xn-2(x2+3)(x2-1)=2xn-2(x2+3)(x+1)(x-1) |
| D、2xn-2(x4-2x2+3)=2xn-2 (x2+3)(x2+1) |
 已知在等边△ABC中,D为AB中点,DE⊥BC于E.求证:BC=4BE.
已知在等边△ABC中,D为AB中点,DE⊥BC于E.求证:BC=4BE.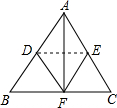 如图,沿DE折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC.△DBF和△EFC是否为等腰三角形?请说明理由.
如图,沿DE折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC.△DBF和△EFC是否为等腰三角形?请说明理由. 如图,已知CD∥BE,且∠D=∠E,试说明AD∥CE的理由.
如图,已知CD∥BE,且∠D=∠E,试说明AD∥CE的理由.