题目内容
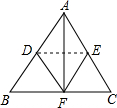如图，沿DE折叠一张三角形纸片ABC，使点A落在BC边上的点F，且折痕DE∥BC．△DBF和△EFC是否为等腰三角形？请说明理由．考点：翻折变换（折叠问题）
专题：
分析：根据翻折变换可得△FDE≌△ADE，于是得∠ADE=∠EDF，∠AED=∠DEF，再由平行线的性质得∠ADE=∠B，∠EDF=∠BFD，∠AED=∠C，∠DEF=∠EFC，进而得∠B=∠BFD，∠C=∠EFC，所以△BDF和△CEF是等腰三角形．
解答：解：△DBF和△EFC是等腰三角形．
∵△FDE由△ADE翻折得到，
∴△FDE≌△ADE，
∴∠ADE=∠EDF，∠AED=∠DEF，
又∵DE∥BC，
∴∠ADE=∠B，∠EDF=∠BFD，∠AED=∠C，∠DEF=∠EFC，
∴∠B=∠BFD，∠C=∠EFC
∴△BDF和△CEF是等腰三角形．
∵△FDE由△ADE翻折得到，
∴△FDE≌△ADE，
∴∠ADE=∠EDF，∠AED=∠DEF，
又∵DE∥BC，
∴∠ADE=∠B，∠EDF=∠BFD，∠AED=∠C，∠DEF=∠EFC，
∴∠B=∠BFD，∠C=∠EFC
∴△BDF和△CEF是等腰三角形．
点评：本题考查翻折变换、平行线及等腰三角形的判定，有一定难度．
练习册系列答案
相关题目
如图，已知B是EC的中点，∠ABE=∠DBC，∠A=∠D，求证：DE=AC．