题目内容
5.下列选项中正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C. | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D. | 若a>0,则$\sqrt{a^2}=a$ |
分析 分别利用二次根式加减运算法则以及分式的基本性质、二次根式的性质判断得出答案.
解答 解:A、$\sqrt{2}$+$\sqrt{3}$无法计算,故此选项错误;
B、$\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{y}{2x}$,故此选项错误;
C、$\frac{n}{m}$=$\frac{n-a}{m-a}$(m≠a),故此选项错误;
D、若a>0,则$\sqrt{{a}^{2}}$=a,故此选项正确.
故选:D.
点评 此题主要考查了二次根式加减运算以及分式的基本性质、二次根式的性质等知识,正确掌握相关运算法则是解题关键.

练习册系列答案
相关题目
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
13.用配方法解方程3x2-$\frac{12}{5}$x-1=0时,变形正确的是( )
| A. | (x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | B. | 3(x+$\frac{2}{5}$)2-$\frac{37}{25}$=0 | C. | (x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 | D. | 3(x-$\frac{2}{5}$)2-$\frac{37}{25}$=0 |
10.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
17.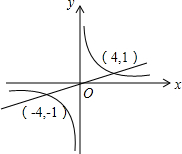 如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
 如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )| A. | -4<x<0或x>4 | B. | -4>x或0<x<4 | C. | -4<x<4且x≠0 | D. | x<-4或x>4 |
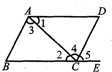 如图,下列条件中:
如图,下列条件中: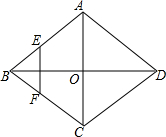 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.
如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的面积为4$\sqrt{3}$.