题目内容
7.写出一个直角坐标系中第二象限内点的坐标:(-1,1).(任写一个只要符合条件即可)分析 根据第二象限内点的横坐标是负数,纵坐标是正数解答.
解答 解:第二象限内点的坐标(-1,1)(任写一个只要符合条件即可).
故答案为:(-1,1).
点评 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
18.下列式子中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{8}$=4 | B. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | C. | $\sqrt{\frac{4}{3}}$=$\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{4\sqrt{18}}{2\sqrt{6}}$=2$\sqrt{3}$ |
15.若M(-2,y1),N(-1,y2),P(2,y3)三点都在函数y=$\frac{k}{x}$(k<0)的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y2>y1>y3 |
17.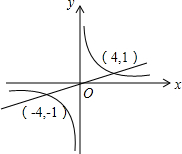 如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
 如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )
如图,直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于(-4,-1)和(4,1),则不等式$\frac{1}{4}$x>$\frac{4}{x}$的解集为( )| A. | -4<x<0或x>4 | B. | -4>x或0<x<4 | C. | -4<x<4且x≠0 | D. | x<-4或x>4 |
 如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.
如图,A,B是4×4网格上的两个格点,在格点中任意放置点C,与点A,点B恰好围成等腰三角形的概率是$\frac{9}{25}$.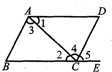 如图,下列条件中:
如图,下列条件中: