题目内容
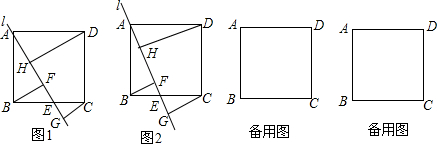
17.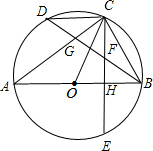 如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.
如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.(1)求证:CF=BF=GF;
(2)若CD=6,AC=8,求圆O的半径和BD长.
分析 (1)根据C是弧BD的中点,可以确定∠A=∠DBC;再根据AB是⊙O的直径,可知∠ACB=90°;据此即可确定∠A=∠DBC,即∠ECB=∠DBC,根据等角对等边得出CF=BF,然后根据∠DBC+∠CGB=90°,∠ECB+∠GCF=90°得出∠CGB=∠GCF,即可得出结论;
(2)根据C是弧BD的中点,得出BC=CD=6,根据勾股定理即可求得半径,根据垂径定理得出OC垂直平分BD,设OG=x,则CG=5-x,根据勾股定理得出52-x2=62-(5-x)2,求得OG,然后根据勾股定理求得BG,进而求得BD.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠A=∠ECB,
∵C是弧BD的中点,
∴∠A=∠DBC,
∴∠ECB=∠DBC,
∴CF=BF,
∵∠DBC+∠CGB=90°,∠ECB+∠GCF=90°,
∴∠CGB=∠GCF,
∴CF=GF,
∴CF=BF=GF;
(2)解:∵C是弧BD的中点,
∴BC=CD=6,
∵AC=8,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10,
∴圆O的半径是5,
∵$\widehat{DC}$=$\widehat{BC}$,
∴OC垂直平分BD,
设OG=x,则CG=5-x,
∵BG2=OB2-OG2=BC2-CG2,
∴52-x2=62-(5-x)2,
解得x=1.4,
∴OG=1.4,
∴BG=$\sqrt{O{B}^{2}-O{G}^{2}}$=4.8,
∴BD=2BG=9.6.
点评 本题是综合考查了圆周角定理、垂径定理、勾股定理以及等腰三角形的判定等;熟练掌握这些定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.在下列各式子$\frac{1}{2}ab,\frac{n}{m},s=π{R^2},\frac{1}{b}(x-y),3,{a^2}+2ab+{b^2}$中,代数式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
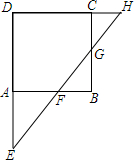 在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$
在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$