题目内容
15.阅读计算:阅读下列各式:(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4…
回答下列三个问题:
(1)验证:(4×0.25)100=1;4100×0.25100=1.
(2)通过上述验证,归纳得出:(ab)n=anbn;(abc)n=anbncn.
(3)请应用上述性质计算:(-0.125)2015×22014×42014.
分析 ①先算括号内的,再算乘方;先乘方,再算乘法.
②根据有理数乘方的定义求出即可;
③根据同底数幂的乘法计算,再根据积的乘方计算,即可得出答案.
解答 解:①:(4×0.25)100=1100=1;4100×0.25100=1,
故答案为:1,1.
②(a•b)n=anbn,(abc)n=anbncn,
故答案为:anbn,(abc)n=anbncn.
③原式=(-0.125)2012×22012×42012×(-0.125)
=(-0.125×2×4)2012×(-0.125)
=(-1)2012×(-0.125)
=1×(-0.125)
=-0.125.
点评 本题考查了同底数幂的乘法,再根据积的乘方,有理数乘方的定义的应用,主要考查学生的计算能力.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
3.在数轴上表示-13的点与表示-4的点之间的距离是( )
| A. | 9 | B. | -9 | C. | 15 | D. | -15 |
7.在下列各式子$\frac{1}{2}ab,\frac{n}{m},s=π{R^2},\frac{1}{b}(x-y),3,{a^2}+2ab+{b^2}$中,代数式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4. 如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )
如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )
 如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )
如图,BE、CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,BE、CF相交于D,则∠BDC的度数是( )| A. | 110° | B. | 70° | C. | 80° | D. | 75° |

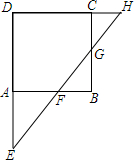 在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$
在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$