题目内容
9. 如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论.
如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论.
分析 根据等腰三角形的性质得到AD⊥BC,∠BAD=∠CAD=$\frac{1}{2}$∠BAC,由BE⊥AC,于是得到∠C+∠CAD=∠C+∠CBE=90°,推出∠CBE=∠CAD=$\frac{1}{2}∠$BAC,由于BF平分∠ABE,于是得到∠FBE=$\frac{1}{2}$∠ABE=$\frac{1}{2}$(90°-∠BAC),求出∠DBF=∠DBE+∠FBE=$\frac{1}{2}$∠BAC+$\frac{1}{2}$(90°-∠BAC)=45°,于是得到结论.
解答 解:△DBF是等腰直角三角形,
理由:∵AB=AC,点D是BC的中点,
∴AD⊥BC,∠BAD=∠CAD=$\frac{1}{2}$∠BAC,
∴∠ADB=90°,
∵BE⊥AC,
∴∠C+∠CAD=∠C+∠CBE=90°,
∴∠CBE=∠CAD=$\frac{1}{2}∠$BAC,
∵BF平分∠ABE,
∴∠FBE=$\frac{1}{2}$∠ABE=$\frac{1}{2}$(90°-∠BAC),
∴∠DBF=∠DBE+∠FBE=$\frac{1}{2}$∠BAC+$\frac{1}{2}$(90°-∠BAC)=45°,
∴△DBF是等腰直角三角形.
点评 本题考查了等腰直角三角形的判定,等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
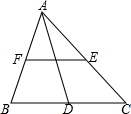 如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).
如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).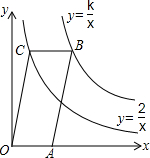 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4. 如图,已知∠1=∠2=75°,∠A=45°,且∠C=∠D,求∠F和∠DEC的度数.
如图,已知∠1=∠2=75°,∠A=45°,且∠C=∠D,求∠F和∠DEC的度数. 如图,是作∠AOB的平分线的另一种方法,以O为圆心,适当长为半径作两条弧分别交边OA于C、E,交边OB于D、F,再连接DE、CF相交于P,作射线OP,则OP为∠AOB的平分线,那么图中有( )对全等三角形(不在添加辅助线).
如图,是作∠AOB的平分线的另一种方法,以O为圆心,适当长为半径作两条弧分别交边OA于C、E,交边OB于D、F,再连接DE、CF相交于P,作射线OP,则OP为∠AOB的平分线,那么图中有( )对全等三角形(不在添加辅助线).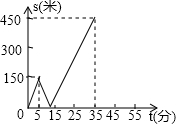 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙出发沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示,下列说法:
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙出发沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示,下列说法: