题目内容
19.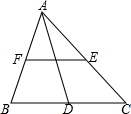 如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).
如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).
分析 先根据三角形中位线定理得出EF∥BC,EF=$\frac{1}{2}$BC,由中线的定义得到BD=$\frac{1}{2}$BC,等量代换得到BD=EF,再根据一组对边平行且相等的四边形是平行四边形得出四边形BDEF是平行四边形;同理得出四边形CDFE,AEDF是平行四边形.
解答  解:四边形BDEF,CDFE,AEDF是平行四边形.理由如下:
解:四边形BDEF,CDFE,AEDF是平行四边形.理由如下:
连结DE、DF.
∵EF为△ABC的中位线,AD为BC边上的中线,
∴EF∥BC,EF=$\frac{1}{2}$BC,BD=$\frac{1}{2}$BC,
∴BD=EF,
即EF∥BD,BD=EF,
∴四边形BDEF是平行四边形;
同理得出四边形CDFE,AEDF是平行四边形.
点评 本题考查了平行四边形的判定,三角形中位线定理,用到的知识点:
一组对边平行且相等的四边形是平行四边形;三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
 如图,设P为△ABC内一点,且PC=BC,求证:AB>AP.
如图,设P为△ABC内一点,且PC=BC,求证:AB>AP.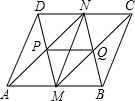 如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题:
如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题: 如图,在梯形ABCD中,AB∥CD,AB=15,CD=30,点E,F分别为AD,BC上一点,且EF∥AB.若梯形AEFB∽梯形EDCF,求线段EF的长.
如图,在梯形ABCD中,AB∥CD,AB=15,CD=30,点E,F分别为AD,BC上一点,且EF∥AB.若梯形AEFB∽梯形EDCF,求线段EF的长. 如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论.
如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论.