题目内容
14.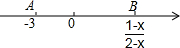 (1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016.
(1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016.(2)如图,点A,B在数轴上,它们所对应的数分别是-3和$\frac{1-x}{2-x}$,且点A,B到原点的距离相等,求x.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可;
(2)根据点A,B到原点的距离相等可得出$\frac{1-x}{2-x}$=3,求出x的值即可.
解答 解:(1)原式=$\frac{x-1}{x}$•$\frac{(x+1)(x-1)}{(x-1)^{2}}$
=$\frac{x-1}{x}$•$\frac{x+1}{x-1}$
=$\frac{x+1}{x}$,
当x=2006时,原式=$\frac{2016+1}{2016}$=$\frac{2017}{2016}$;
(2)∵点A,B到原点的距离相等,
∴$\frac{1-x}{2-x}$=3,
方程两边同时乘以2-x得,1-x=3(2-x),解得x=$\frac{5}{2}$,
经检验,x=$\frac{5}{2}$是原分式方程的根.
点评 本题考查的是分式的化简求出,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )
 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )| A. | ab-π($\frac{b}{2}$)2 | B. | ab-$\frac{π{b}^{2}}{2}$ | C. | ab-$π(\frac{a}{2})$2 | D. | ab-$\frac{π}{2}$($\frac{b}{2}$)2 |
2.已知a=$\frac{1}{2+\sqrt{3}}$,b=2-$\sqrt{3}$,则a与b的大小关系是( )
| A. | a>b | B. | a=b | C. | a<b | D. | 不确定 |
4. 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )| A. | 60° | B. | 80° | C. | 50° | D. | 75° |
 已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.
已知:菱形OBCD在平面直角坐标系中位置如图所示,点B的坐标为(2,0),∠DOB=60°.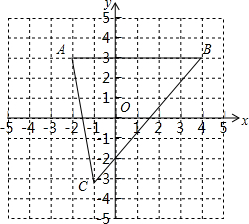 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3).