题目内容
19.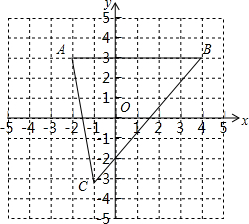 如图,已知A(-2,3)、B(4,3)、C(-1,-3).
如图,已知A(-2,3)、B(4,3)、C(-1,-3).(1)求点C到x轴的距离;
(2)分别求△ABC的三边长;
(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.
分析 (1)直接利用C点坐标得出点C到x轴的距离;
(2)利用A,C,B的坐标分别得出各边长即可;
(3)利用△ABP的面积为6,得出P到AB的距离进而得出答案.
解答  解:(1)∵C(-1,-3),
解:(1)∵C(-1,-3),
∴点C到x轴的距离为:3;
(2)∵A(-2,3)、B(4,3)、C(-1,-3),
∴AB=4-(-2)=6,
AC=$\sqrt{{1}^{2}+{6}^{2}}$=$\sqrt{37}$,BC=$\sqrt{{5}^{2}+{6}^{2}}$=$\sqrt{61}$;
(3)∵点P在y轴上,当△ABP的面积为6时,
∴P到AB的距离为:6÷($\frac{1}{2}$×6)=2,
故点P的坐标为:(0,1),(0,5).
点评 此题主要考查了三角形的面积以及勾股定理等知识,得出P到AB的距离是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x-3)=7
以下是王萌同学的作业:
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x-3)=7
以下是王萌同学的作业:
| 解:(1)移项,得x(x+1)-2x=0 分解因式得,x(x+1-2)=0 所以,x=0,或x-1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x-3)=1×7 所以,x+1=7,x-3=1 解得,x1=6,x2=4 |
4.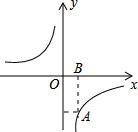 如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )
如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )
 如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )
如图,函数y=$\frac{k}{x}$的图象经过点A(1,-3),AB垂直x轴于点B,则下列说法正确的是( )| A. | k=3 | B. | x<0时,y随x增大而增大 | ||
| C. | S△AOB=3 | D. | 函数图象关于y轴对称 |
8. 如图,a、b是有理数,则下列结论正确的是( )
如图,a、b是有理数,则下列结论正确的是( )
 如图,a、b是有理数,则下列结论正确的是( )
如图,a、b是有理数,则下列结论正确的是( )| A. | -b<-a<a<b | B. | -a<-b<a<b | C. | -b<a<-a<b | D. | -b<b<-a<a |
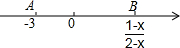 (1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016.
(1)先化简,再求值:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$,其中x=2016. 如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为$\widehat{AD}$的中点,连结CE交AB于点F,且BF=BC.
如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为$\widehat{AD}$的中点,连结CE交AB于点F,且BF=BC.