Question

9．已知：菱形OBCD在平面直角坐标系中位置如图所示，点B的坐标为（2，0），∠DOB=60°．
（1）点D的坐标为（1，$\sqrt{3}$），点C的坐标为（3，$\sqrt{3}$）；
（2）若点P是对角线OC上一动点，点E（0，-$\sqrt{3}$），求PE+PB的最小值．

Answer 1

分析 （1）作DF⊥OB于点F，在直角△ODF中利用三角函数求得DF和OF的长，则D的坐标即可求得，然后根据CD∥OB，则C的坐标即可求得；
（2）B关于OC的对称点是D，则DE的长就是PE+PB的最小值，作DH⊥y轴于点H，首先在直角△OGH中利用勾股定理求得DH和OH的长，然后在直角△HED中利用勾股定理求解．

解答 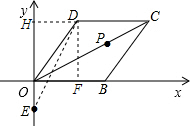解：（1）作DF⊥OB于点F．
∵B的坐标是（2，0），
∴OB=2，
∴菱形OBCD中，OD=OB=CD=2，
在直角△ODF中，DF=OD•sin∠DOB=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，OF=OD•cos∠DOB=2×$\frac{1}{2}$=1，
则D的坐标是（1，$\sqrt{3}$）．
则C的坐标是（3，$\sqrt{3}$）．
故答案是：（1，$\sqrt{3}$），（3，$\sqrt{3}$）；
（2）作DH⊥x轴于点H，连接DE．
在直角△OGH中，∠HOG=90°-∠DOB=90°-60°=30°．
GH=OD•sin∠HOG=2×$\frac{1}{2}$=1，OH=OG•cos∠HOG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$．
则HE=2$\sqrt{3}$．
在直角△HEG中，DE=$\sqrt{H{G}^{2}+H{E}^{2}}$=$\sqrt{{1}^{2}+（2\sqrt{3}）^{2}}$=$\sqrt{13}$．
即PE+PB的最小值是$\sqrt{13}$．

点评 本题考查了菱形的性质以及路径最短问题，根据菱形的对称性确定PE+PB最小的条件是关键．