题目内容
18.若$\sqrt{x-5}$+y=3,则$\sqrt{{x}^{2}-10x+25}$-$\sqrt{{y}^{2}-6y+9}$=x+y-8.分析 首先得出x-5,3-y进而化简求出即可.
解答 解:∵$\sqrt{x-5}$+y=3,
可得:x-5>0,3-y>0,
故$\sqrt{{x}^{2}-10x+25}$-$\sqrt{{y}^{2}-6y+9}$=x-5-(3-y)=x+y-8.
故答案为:x+y-8.
点评 此题主要考查了二次根式的化简求值,得出各项符号是解题关键.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a2×a3=a6 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a2)3=a5 |
7.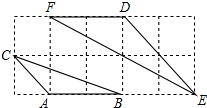 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
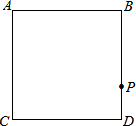 已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动,
已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动, 在一次数学活动课上,老师将一块等腰直角三角形纸片PMN的直角顶点P放在正方形ABCD的对角线BD上,使直角边PM经过正方形的顶点C,另一直角边PN与AB交于点E,如图所示,问:CE和MN存在怎样的位置关系.
在一次数学活动课上,老师将一块等腰直角三角形纸片PMN的直角顶点P放在正方形ABCD的对角线BD上,使直角边PM经过正方形的顶点C,另一直角边PN与AB交于点E,如图所示,问:CE和MN存在怎样的位置关系.