题目内容
8.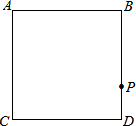 已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动,
已知四边形ACDB为正方形,P是正方形边上任意一点,若P运动的方向为逆时针运动,(1)当运动到边AB上时,△PCD的面积最大;
(2)当点P运动到线段AB的时候,△PCD的面积没有改变,理由是同底等高的三角形面积相等.
分析 (1)根据三角形的面积公式S△PCD=$\frac{1}{2}$CD×高,由CD的值固定,所以当△PCD的面积最大时,即CD边上的高最大,即点P运动到边AB上时,△PCD的面积最大;
(2)根据同底等高的三角形面积相等即可说理.
解答 解:(1)∵S△PCD=$\frac{1}{2}$CD×高,且CD的值固定,
∴当CD边上的高最大时,△PCD的面积最大,
即点P运动到边AB上时,△PCD的面积最大;
故答案为:边AB上;
(2)∵当点P运动到线段AB的时候,
点P到CD的距离不变,即△PCD的高不变,且底CD的值固定不变.
∴当点P运动到线段AB的时候,△PCD的面积没有改变,
即同底等高的三角形面积相等.
故答案为:同底等高的三角形面积相等.
点评 此题考查了三角形的面积,解题的关键是:明确同底等高的三角形面积相等.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.下列说法错误的是( )
| A. | 若△ABC中,a2=(b+c)(b-c),则△ABC是直角三角形 | |
| B. | 若△ABC中,a2+b2≠c2,则△ABC不是直角三角形 | |
| C. | 若△ABC中,a:b:c=13:5:12,则∠A=90° | |
| D. | 若△ABC中,a、b、c三边的长分别为n2-1、2n、n2+1(n>1),则△ABC是直角三角形 |
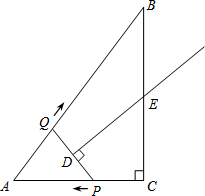 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).