题目内容
13.求证:对于任意的正整数n,3n+2-2n+2+3n-2n一定是10的倍数.分析 首先首先把底数相同的提取公因式,分解因式,进一步探讨是不是10的倍数即可.
解答 解:∵3n+2-2n+2+3n-2n
=3n+2+3n-2n+2-2n
=3n(32+1)-2n(22+1)
=10×3n-10×2n-1
=10×(3n-2n-1)
∴3n+2-2n+2+3n-2n一定是10的倍数.
点评 此题考查因式分解在实际中的运用,注意分类,进一步利用提取公因式法因式分解.

练习册系列答案
相关题目
1.已知方程组$\left\{\begin{array}{l}2x+y=-1\\ x+y=0\end{array}\right.$的解是$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$,那么以$\left\{\begin{array}{l}x=-1\\ y=1\end{array}\right.$为解的二元一次方程组有( )
| A. | 有且只有1个 | B. | 有且只有2个 | C. | 不可能有3个 | D. | 有无数个 |
5.在二次函数y=-$\frac{1}{12}$(x-2)2+3的图象上有两点(-1,y1),(1,y2),则y1-y2的值是( )
| A. | 负数 | B. | 零 | C. | 正数 | D. | 不能确定 |
3.下列实数中,最大的是( )
| A. | -1 | B. | -2 | C. | -$\sqrt{2}$ | D. | -$\frac{4}{3}$ |
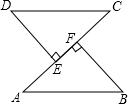 如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.
如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.