Question

7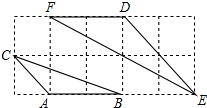．如图，如果△ABC与△DEF都是正方形网格中的格点三角形（顶点在格点上），那么△DEF与△ABC的周长比为（　　）

• A． 4：1
• B． 3：1
• C． 2：1
• D． $\sqrt{2}$：1

Answer 1

分析 如图，设正方形网格的边长为1，根据勾股定理求出△EFD、△ABC的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△EDF∽△BAC，即可解决问题．

解答 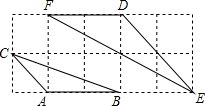解：如图，设正方形网格的边长为1，由勾股定理得：
DE²=2²+2²，EF²=2²+4²，
∴DE=2$\sqrt{2}$，EF=2$\sqrt{5}$；
同理可求：AC=$\sqrt{2}$，BC=$\sqrt{10}$，
∵DF=2，AB=2，
∴$\frac{EF}{BC}=\frac{DE}{AB}=\frac{DF}{AC}=\sqrt{2}$，
∴△EDF∽△BAC，
∴l_△DEF：l_△ABC=$\sqrt{2}$：1，
故选D．

点评 本题主要考查了勾股定理和相似三角形的判定及其性质定理的应用问题；应牢固掌握有关定理，这是灵活运用解题的关键；对综合的分析问题解决问题的能力提出了较高的要求．