题目内容
9.已知Rt△ABC,∠C=90°,AC=3,BC=6,则△ABC的外接圆面积是$\frac{45}{4}π$.分析 根据勾股定理求出斜边,根据直角三角形的外接圆的半径等于斜边的一半求出即可.
解答 解:由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∵△ACB是直角三角形,
∴△ABC的外接圆半径长为斜边的一半,即是$\frac{3\sqrt{5}}{2}$,
则△ABC的外接圆面积是:π($\frac{3\sqrt{5}}{2}$)2=$\frac{45}{4}$π.
故答案为:$\frac{45}{4}π$.
点评 本题考查了勾股定理和直角三角形的外接圆的应用,注意:直角三角形的外接圆的半径等于斜边的一半.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
13.下列说法错误的是( )
| A. | 若△ABC中,a2=(b+c)(b-c),则△ABC是直角三角形 | |
| B. | 若△ABC中,a2+b2≠c2,则△ABC不是直角三角形 | |
| C. | 若△ABC中,a:b:c=13:5:12,则∠A=90° | |
| D. | 若△ABC中,a、b、c三边的长分别为n2-1、2n、n2+1(n>1),则△ABC是直角三角形 |
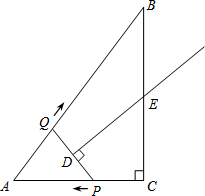 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).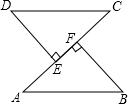 如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.
如图,已知AB=CD,DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF.