题目内容
20.已知直角三角形中一条直角边长为4,如果斜边长与另一条直角边长的和是10,求斜边上的中线长.分析 设斜边的长为xcm,则另一直角边长为(10-x)cm,再根据勾股定理求出x的值,进而可求出斜边上的中线长.
解答 解:设斜边的长为xcm,则另一直角边长为(10-x)cm,
∵直角三角形的一条直角边长是4cm,
∴42+(10-x)2=x2,
解得x=5.8.
∴斜边上的中线长=$\frac{1}{2}$×5.8=2.9.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 尺规作图:把如图(实线部分)补成以虚线m为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案.(不用写作法,保留作图痕迹).
尺规作图:把如图(实线部分)补成以虚线m为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案.(不用写作法,保留作图痕迹).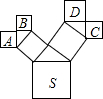 如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是25cm2.
如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是25cm2.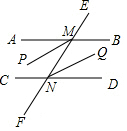 已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.
已知:如图,AB∥CD,AB,CD与直线EF分别相交于点M和N,MP平分∠AMF,NQ平分∠DNE.求证:MP∥NQ.