题目内容
8.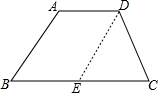 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )| A. | AB∥DE且AB=DE | B. | ∠DEC=∠B | C. | AD∥EC且AD=EC | D. | BC=AD+EC |
分析 利用平移的性质得到四边形ABED是平行四边形,然后利用平行四边形的性质分别判断后即可确定正确的选项.
解答 解:∵将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,
∴AD∥BC,AD=BE,
∴四边形ABED是平行四边形;
∴A、AB∥DE且AB=DE正确;
B、∠DEC=∠B,正确;
C、AD∥EC但AD=EC不一定成立,故错误;
D、BC=BE+EC=AD+EC,故正确,
故选C.
点评 本题考查了平移的性质,解题的关键是了解平移前后的只有位置的变化,能判定四边形ABED是平行四边形是解答本题的关键,难度不大.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
19.一次函数y=kx+k,且y随x的增大而减小,那么反比例函数y=$\frac{k}{x}$满足( )
| A. | 当x>0时,y>0 | B. | 在每个象限内,y随x的增大而减小 | ||
| C. | 图象分布在第一、三象限 | D. | 图象分布在第二、四象限 |
16.不等式组$\left\{\begin{array}{l}{x-2>0}\\{\frac{x}{2}≤4}\end{array}\right.$的解集是( )
| A. | x≥8 | B. | x>2 | C. | 0<x<2 | D. | 2<x≤8 |
13.下列说法正确的有( )个
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.已知两直线y1=kx+k-1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是$\frac{2013}{4028}$.
18.(2+1)(22+1)(24+1)(28+1)…(232+1)+1 的个位数字为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
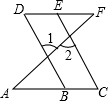 如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?
如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D.∠ABD与∠C相等吗?为什么?